Brief intro to NFA, DFA and regexes

Finite State Automata

Finite State Automata are abstract models of computation. In other words, they are sytems that take input (in form of symbols) and spit out a result (or, perform a computation). To do this, they read symbols and move internally between states. They can be described by 3 things:

• starting state
• list of states
• transitions between states

‘Transitions between states’ can also be thought of as a function that takes as arguments the current state and current symbol and returns what the next state should be.

function transition(current_state, symbol) {
     ...
     return next_state;
}

Easy.

There are two types of automata:

           FSA
         /    \
        /      \
      DFA       NFA

Let’s look at them!

Deterministic Finite Automata

DFA stands for Deterministic Finite Automaton. Its job is to read in a string of symbols (input) and move (transition) between its states based on the input and ultimately accept or reject the string of symbols. The transitions are deterministic: for a given symbol string and a given DFA, the DFA will go through the same states every time the same symbol string is fed into it. In other words, the path between the states is guaranteed to be unique for a given symbol string. The way this is enforced is by specifying that for every state, for a given input symbol, there’s only one transition. So this is allowed:

Figure 1 : DFA example.

but this is not:

Figure 2 : NFA example. By Ashutosh y0078 - Own work, CC BY-SA 3.0, Wikimedia link

Because from starting state p we can move to both q and back to p on receiving 1 as an input, this cannot be (by definition) a deterministic automata. This, in fact, is an NFA.

Non-Deterministic Finite Automaton

NFA is non-deterministic finite automaton. In an NFA:

• in a state, for one input, the automaton can transition to more than one states
• automaton can transition using empty input

Let’s look at another NFA.

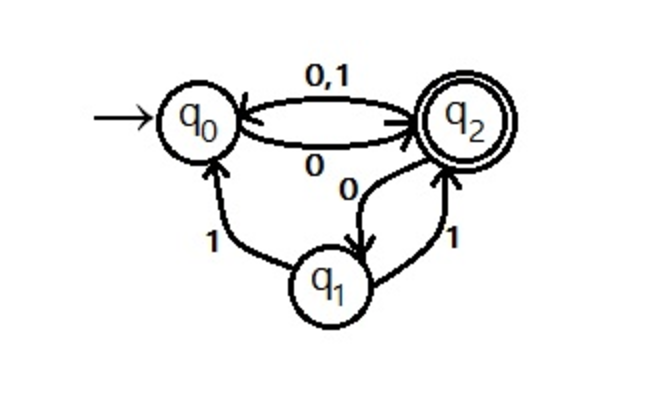
Figure 3 : Another NFA. Example taken from: http://er.yuvayana.org/

NFAs are smaller than DFA, in terms of number of states. Remember the rule that a string of symbols follow a unique path between states in a DFA? That does not apply in an NFA. For example, if the NFA in Figure 3 is in state q₂, then if it reads in symbol 1, it could go to either q₀ or q₁. It’s not deterministic (as the name implies). However, an NFA can always be converted into a DFA - there are algorithms for it - it will just have more states. This should be intuitive - if I am restricted to only one transition per symbol per state, then to encode the same behaviour as an NFA (with multiple transitions allowed per symbol per state), I will need more states. Let’s see what happens when we convert Figure 3 NFA to DFA (the proof is left as an exercise to the reader. Listing the steps of the algorithm used does not make for a brief introduction, and is just application of the algorithm - not very interesting. The important thing to note is that a) it is possible, and b) the NFA is smaller than its equivalent DFA.)

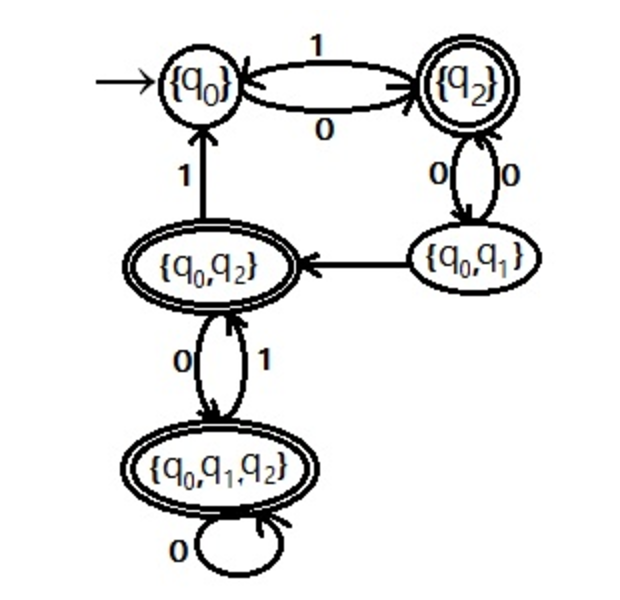
Figure 4 : Figure 3 NFA converted to DFA. Example taken from: http://er.yuvayana.org/

DFAs and NFAs (or more generally, FSAs) recognize regular languages. In fact, they exactly recognize regular languages - every regular language has an finite state automaton that accepts it. Which brings us to regular expressions.

Regular Expressions

Regular expressions are a way of expressing regular languages. In fact, the basic operation of a regex engine is to convert a regex pattern to either an NFA or DFA internally. Then, faced with a string, the N/DFA reads the symbols one by one and transitions between its states and finally spits out if the string of symbols matches the pattern/language or not.

Now, the interesting part. Remember: the purpose of an FSA is to check if a string of symbols can be accepted. If given a regular language that is described by an NFA and a DFA (as we can always convert an NFA -> DFA), the DFA will take (in principle) less time than the NFA to check if a string of symbols is accepted by the language. This is because at every state of a DFA, for a given input symbol, it’s clear what next step to take. However, with an NFA, a depth-first search is required to check every possible combination. So we trade space for time when we use a DFA instead of an NFA!

Interesting Stack Overflow question on how to check if a regex engine uses an NFA or DFA internally.